|
Note
|
The authors assume no responsibility or liability for any errors or omissions in the content of this documentation. The information contained in this documentation is provided on an "as is" basis with no guarantees of completeness, accuracy, usefulness, timeliness or of the results obtained from the use of this information. |
This Guide refers to the OpenWebStart version 1.14.0-SNAPSHOT and was build at 31.12.2025.
Introduction
Java Web Start (JWS) was deprecated in Java 9, and starting with Java 11, Oracle removed JWS from their JDK distributions. This means that clients that have the latest version of Java installed can no longer use JWS-based applications. And since public support of Java 8 has ended in Q2/2019, companies no longer get any updates and security fixes for Java Web Start.
This is why some enthusiasts at Karakun decided to create OpenWebStart, an open source reimplementation of the Java Web Start technology. This guide describes how you can use OpenWebStart as a replacement for JWS and continue using your JNLP-based applications with little or no change at all.
We appreciate your feedback. If you feel that there’s a lack of documentation in a certain area or if you find inaccuracies in the documentation, please don’t hesitate to contact us at openwebstart@karakun.com or the support forum.
What is OpenWebStart?
OpenWebStart is an open source reimplementation of the Java Web Start technology, released under the GPL with Classpath Exception. It provides the most commonly used features of Java Web Start and the JNLP standard, so that your customers can continue using applications based on Java Web Start and JNLP without any change. OpenWebStart is based on Iced-Tea-Web and follows the JNLP-specification defined in JSR-56.
The focus of OpenWebStart is the execution of JNLP-based applications. Additionally, the tool contains various modules that simplify your Web Start workflows and let you configure OpenWebStart to suit your needs:
- App Manager
-
Manages the versions of any JNLP-based application that is executed by OpenWebStart.
- JVM Manager
-
Manages Java versions and Java updates on the client.
- Control Panel
-
Provides a graphical user interface to configure OpenWebStart.
- Updater
-
Downloads and installs new versions of OpenWebStart.
Installation
OpenWebStart can be installed on Windows, MacOS and Linux operating systems and there are two different ways to install OpenWebStart:
-
Using the interactive installation with auto-update functionality
-
Using the unattended installation for automated roll-outs
If you use Web Start for several small customers or on your own, we recommend using the interactive installer. Our native installer will set up everything on your Windows, Mac, or Linux system so that OpenWebStart is immediately ready to use. OpenWebStart checks for updates automatically, and the Updater component keeps the tool current without the need for any user interaction.
If you or your customers are companies with IT departments of their own, we recommend an unattended installation to roll out OpenWebStart on multiple client machines with similar configuration. Instead of walking through the graphical installer of OWS on every machine your IT department can pre-define the responses for the installation options in a response varfile.
Interactive Installation
Windows
-
Open the ZIP-file.
-
Run the installer.
-
Accept the license
-
Click Next and choose whether to install for the current user or for all users.
-
Click Next to start the OpenWebStart installation.
-
Browse to the directory where to install OpenWebStart, and click Next.
Windows default:C:\Program Files\OpenWebStart -
Select the checkbox to associate the .JNLP and .JNLPX suffixes with OpenWebStart, and click Next.
-
Please wait for OpenWebStart to be installed on your computer.
-
Click Finish on the completion screen to close the wizard.
macOS
-
Open the OpenWebStart disk image (DMG file) to mount it.
-
Run the
Open Web Start Installer.app. -
Accept the license
-
Click Next and choose whether to install for the current user or for all users.
-
Click Next to start the OpenWebStart installation.
-
Browse to the directory where to install OpenWebStart, and click Next.
Default:/Applications/Open Web Start -
The installer automatically adds to info.plist file of OpenWebStart javaws the associations for .JNLP and .JNLPX suffixes.
In case .JNLP is associated with Oracle javaws, you may have to manually make the association ot OWS javaws:
Open Finder, find a .jnlp file, choose it, press cmd+shift+i to open File Info, change "Open with" to OpenWebStart, press "Change all" -
Please wait for OpenWebStart to be installed on your computer.
-
Click Finish on the completion screen to close the wizard.
-
Please also check the https://openwebstart.com/docs/FAQ.html[FAQ]
Linux
-
Go to the directory where the installer (DEB file) is stored and run the file from the terminal
sudo dpkg -i OpenWebStart_linux_1_1_8.deb -
Enter your root password.
-
Accept the license
-
Click Next to start the OpenWebStart installation.
-
Browse to the directory where to install OpenWebStart, and click Next.
Default:/opt/openwebstart -
Enable the checkbox to associate the .JNLP and .JNLPX suffixes with OpenWebStart, and click Next.
-
Please wait for OpenWebStart to be installed on your computer.
-
Click Finish on the completion screen to close the wizard.
If you need help to install OpenWebStart, also have a look at the public installation and configuration discussions at the Support Forum.
Installation Artifacts
The artifacts of an installed release are the follows:
- OpenWebStart main executable
-
Application to launch a JNLP file.
-
javaws.exe (Windows),
-
OpenWebStart javaws.app (macOS)
-
- OpenWebStart settings executable
-
Application to configure your OpenWebStart installation.
-
itw-settings.exe (Windows),
-
OpenWebStart Settings.app (macOS)
-
- Uninstaller executable
-
Application to uninstall OpenWebStart from your system.
-
uninstall.exe (Windows)
-
OpenWebStart Uninstaller.app (macOS)
-
- jre directory (Windows)
-
The bundled JRE that starts OpenWebStart
- javaws.vmoptions
-
JVM arguments used by the bundled JRE when starting OpenWebStart main executable (javaws)
- itw-settings.vmoptions
-
JVM arguments used by the bundled JRE when starting OpenWebStart settings executable (itw-settings)
- .install4J directory
-
Contains install4j installer files including response.varfile used for the unattended installation.
- openwebstart.jar
-
OpenWebStart application jar
- *.png
-
Some icons used by OpenWebStart
- readme.txt
-
Describes OpenWebStart release contents and useful links
Unattended Installation
An unattended installation allows for a silent installation and does not prompt you for any input. Use a silent installation when there are similar installations to be performed on more than one computer. In this scenario, the auto-update functionality is inactive; your IT department is free to plan and handle rollouts of new versions based on your internal workflows.
When installing OpenWebStart, several properties can be predefined in a so-called response.varfile file.
Some supported properties are lockable.
If a property is lockable, you can define an additional property of type PROPERTY_NAME.locked=true to prevent users from editing the property in the user interface.
For example, to define a value for the ows.jvm.manager.server.default property that cannot be changed in the user interface, specify the following two properties:
ows.jvm.manager.server.default=https://my.custom.server ows.jvm.manager.server.default.locked=true
Have a look at the Configuration Properties Overview to get an overview of all properties that can be specified in
the response.varfile.
To create a response.varfile file, run the installation of OpenWebStart at least once manually.
By doing so a response.varfile file is created in OpenWebStart installation folder in your system.
In the installation folder, you find a .install4j folder that contains the basic response.varfile file.
Store this file in a location where you can retrieve it later.
The content of such a file looks like this:
sys.adminRights$Boolean=false sys.fileAssociation.extensions$StringArray="jnlp","jnlpx" sys.fileAssociation.launchers$StringArray="313","313" sys.installationDir=/Applications/OpenWebStart sys.languageId=de
You can easily edit this file and add additional properties based on the table in this article.
Do not remove the initial content of the file, change the values as necessary, and add new properties always to the end of the file.
After editing, a response.varfile the file might look like this:
sys.adminRights$Boolean=false sys.fileAssociation.extensions$StringArray="jnlp","jnlpx" sys.fileAssociation.launchers$StringArray="313","313" sys.installationDir=/Applications/OpenWebStart sys.languageId=de ows.jvm.manager.server.default=https://my.custom.server ows.jvm.manager.server.default.locked=true
You can control whether you want to run the installer with admin rights and whether you want to install for the Current User or for All Users by specifying the following properties:
Install For All Users:
userMode$Integer=1
Install For Current User:
userMode$Integer=0
Run the Installer without admin rights:
sys.adminRights$Boolean=false
Run the installer with admin rights:
sys.adminRights$Boolean=true
You can now use your enhanced file to install OpenWebStart on multiple machines.
Simply copy the enhanced response.varfile next to the installer and execute the following command:
- Windows
<OpenWebStart_windows_1.x.x.exe> -q -varfile response.varfile
- MacOS
hdiutil attach OpenWebStart_macos_1_x_x.dmg /Volumes/OpenWebStart/OpenwebStart\ Installer.app/Contents/MacOS/JavaApplicationStub -q -varfile response.varfile hdiutil detach /Volumes/OpenWebStart
Installation Directory for Unattended Installer
For the unattended installation, you may specify the installation directory in response.varfile as follows:
If you specify absolute path, e.g. sys.installationDir=c:\test, then OWS will be installed there.
If you specify relative path, e.g. sys.installationDir=test, then OWS will be installed in the specified directory relative to the directory where the unattended installer command is executed.
If you remove the property sys.installationDir, then for Current User (userMode$Integer=0), OWS will be installed in <User Home>\AppData\Local\Programs directory
and for All Users (userMode$Integer=1) OWS will be installed in C:\Program Files\OpenWebStart directory.
If you would like to install OWS relative to User’s Home directory, you can override sys.installationDir in response.varfile by specifying -dir command line argument as follows:
OpenWebStart_windows-x64_x_x_x.exe -q -varfile response.varfile -dir %USERPROFILE%\<the dir where you want to install ows>
JNLP File Association
To ensure that your computer handles links, desktop shortcuts, or start menu entries to JNLP applications correctly, you should associate the JNLP file type (*.jnlp) on your computer with OpenWebStart.
In case you used an Oracle JVM in the past, your JNLP file association might still be set to Oracle javaws.
Note that during the installation process, OpenWebStart will not change file associations of any existing Oracle javaws executable, so you can use both.
To associate .JNLP applications in Windows Explorer
-
Right-click the JNLP app and select Open With > Choose Another App
-
Click More Apps and scroll down
-
Click Look for Another App on this PC
-
Browse to OpenWebStart at
C:\Program Files\OpenWebStart\javaws -
Click Open to associate this JNLP file with OpenWebStart
To associate .JNLP applications in macOS Finder:
-
Right-click the JNLP app and select Open With > Other…
-
Browse to OpenWebStart at
/Applications/Open Web Start/javaws -
Click Open to associate this JNLP file with OpenWebStart
How to Uninstall
In case you need to uninstall OpenWebStart follow the steps below:
- For Windows and macOS
-
-
Go to your OpenWebStart directory
-
Run the Uninstaller
-
Click Next in the OpenWebstart Uninstaller Wizard
-
Wait for the Uninstaller to complete
-
Click Finish on the completion screen to close the wizard.
-
- For Linux
-
Use your package manager and remove the package OpenWebStart
Running OWS from portable USB stick
It is possible to run OWS from a portable USB stick without actually installing OWS on your machine. Although this is a quick way of running OWS, the downside of not using the installer is that you do not get the support of the underlying operating system in terms of file associations, registry entries and desktop integration. So if you can (and want to) do without the file associations, desktop icon and startup menu you can create a portable version by yourself.
All files required for execution are located in the installation directory (see Installation Artifacts. It is therefore sufficient to copy this directory onto a USB stick and then to run the main executable (Windows: javaws.exe) and settings executable (Windows: itw-settins.exe) by mounting the USB stick on the target computer.
If you want the settings and the cache to also remain on the USB stick, the path to these two directories can be set with the following environment variables:
XDG_CACHE_HOME (default value is %USER_HOME%\.cache)
XDG_CONFIG_HOME (default: %USER_HOME%\.config)To run OWS from a USB stick it is recommended to create a small batch script that sets the two variables and then executes the executables:
javaws.exe [url-to-jnlp | path-to-jnlp] [options]It should also be mentioned that with a new release of OWS the two things that usually change are:
\openwebstart.jar (the application must be updated)
\jre\ (the bundled JRE which is used to run OpenWebStart)So you might want to update these files on the USB stick to keep your OWS installation up-to-date.
Local vs. System-Wide Installation
You can install OWS for the current user (without admin privileges) or for all users (with admin privileges) of the computer.
|
Note
|
Having more than one installation of OWS on your machine, especially when one installation is for current user (i.e. without admin privileges) and the other one is for all users, may result in overwriting registry entries. This can lead to a situation where you do not know which actual OWS is invoked to run the _jnlp file started for example by double-clicking. |
Once OWS is installed on your machine it can be configured locally using the local deployment.properties file
or it can take its configuration from a centralized, enterprise wide deployment.properties file that is specified in the deployment.config file.
This is described in detail in the section on Configuration.
Updates
OpenWebStart can be configured to automatically check for new releases and perform automatic updates.
To do so go to the "Updates" Panel in the OWS Settings.
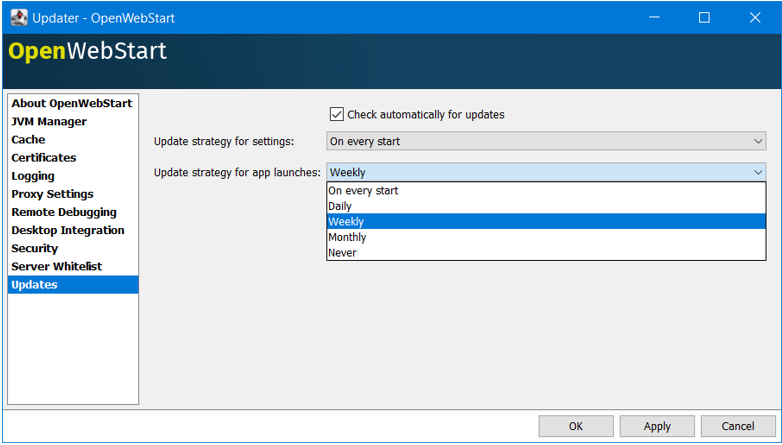
It is possible to define an update strategy on every start, daily, weekly, monthly, or never.
Configuration
OWS can be configured locally using the local deployment.properties file. By default, the deployment.properties is
located in the USER_HOME/.config/icedtea-web directory. However, the user may also place the deployment.properties file
in the OWS installation directory. In this case, the deployment.properties in the OWS installation directory will take
precedence over the default <USER_HOME>/.config/icedtea-web/deployment.properties.
The standard way to configure OpenWebStart is to use the OpenWebStart Settings application.
The executable is located in the installation directory and is named itw-settings.
Various life-cycle aspects of your JNLP applications can be configured, such as download and update strategy or caching behavior. You can configure the JVM vendor and version that should be used to launch your JNLP application as well as proxy settings, security settings, certificates and server whitelists.
Configuration Lookup Lifecycle
When loading the configuration during the start of OpenWebStart the following steps are executed:
-
Load the default values which are hardcoded in the source code.
-
Search for a System Configuration.
-
Load the System Configuration (if one has been specified).
-
Load the User Configuration.
Whenever a configuration is loaded the values which are already defined in a previous lifecycle step are updated. There is however the possibility to lock a property on a system-level lifecycle step. If a property is locked then subsequent configurations may not modify the value. This allows enforcing certain values on a system level. Any changes a user makes in his local user configuration file will not have any effect on a locked property.
User Configuration
The local user configuration properties are stored in a file called deployment.properties.
-
For Windows the file is located at
${USER_HOME}\.config\icedtea-web\deployment.properties. -
For MacOS and Linux the file is located at
${USER_HOME}/.config/icedtea-web/deployment.properties.
This file can be edited with a regular text editor. For some specific configurations manually editing this file might be necessary, but for most cases the OWS Settings application is sufficient.
System Configuration
In an enterprise environment, for uniformity of behavior, it is preferred that all users use the same configuration for OWS.
It is possible to configure OWS with a system-wide configuration. This allows setting up a common configuration for multiple users at a centralized location on a single computer. This helps in managing a corporate infrastructure where many computers need to be configured identically.
Creating a System Configuration
The simplest way to create a system configuration is to start the itw-settings.
After adjusting and saving as you prefer, the configuration the modified properties are written to the local deployment.properties file as described above.
This customized user configuration can be used as a starting point for the system configuration.
Simply copy the file and remove the properties which should not be pre-defined at system-level.
OpenWebStart does not save an entry for a property in the deployment.properties file if it is set to the default value.
Therefore, the generated user configuration may not contain all the values you wish to enforce on the system level.
Where appropriate you have to add additional properties manually.
|
Note
|
Please refer to Configuration Properties Overview for a comprehensive list of deployment properties. |
It is possible to make OWS use deployment.properties from a customized location.
The location of such an optional system-level deployment.properties file is defined in a deployment.config file.
For OWS to find the deployment.config file it must be located in specific location:
-
For Windows in
<Windows Directory>\Sun\Java\Deployment\deployment.config -
For MacOS and Linux in
/etc/.java/deployment/deployment.config
The deployment.config file is a regular properties file.
The following properties can be set to configure the location of the system configuration file:
- deployment.system.config
-
The URL to the system configuration. The name of the system configuration can be freely chosen. Special characters need escaping. See the following examples:
-
deployment.system.config=file\:/C\:/Windows/Sun/Java/global.properties -
deployment.system.config=file\:/etc/.java/deployment/base.properties -
deployment.system.config=https\://192.168.1.1./javaws/system.properties
-
- deployment.system.config.mandatory
-
If set to
truethen OpenWebStart will fail if it is unable to load the system settings This property is optional. The default value isfalse.
The final file should look something like this:
deployment.system.config=https\://192.168.1.1./javaws/system.properties
deployment.system.config.mandatory=trueOWS specific System Configuration
OpenWebStart tries to mimic the behavior of Oracle’s web start (JWS) but it is not exactly the same.
On some systems OpenWebStart is used besides Oracle’s web start.
In such a constellation it is possible that the system configuration needs to be different for Oracle JWS and OWS.
Therefore, OWS allows the user to specify OWS specific deployment.config called itw-deployment.config.
The content of the file is the same as described above. OpenWebStart will pickup
itw-deployment.config while Oracle will use the original deployment.config file.
In the absence of itw-deployment.config OWS uses the original deployment.config.
Locking a Property
One of the use cases is to enforce some configurations to all users in your corporate environment.
This can be achieved by locking configuration on a system level.
To lock a property you need to define a second entry with a .locked postfix.
Here is an example:
ows.jvm.manager.server.default=https\://192.168.1.1/jvms.json
ows.jvm.manager.server.default.locked=true|
Tip
|
the value of ows.jvm.manager.server.default.locked is ignored.
The presence of the key is sufficient for locking the property.
|
System-wide trust store for trusted certificates
OWS has a property deployment.system.security.trusted.certs
to point to a trust store where OWS will look for trusted certificates.
Suppose your trusted certificates are stored in a trust store called trusted.certs. You can copy this file to a central location.
The property deployment.system.security.trusted.certs can be specified in a system level deployment properties
file, e.g. itw.properties :
deployment.system.security.trusted.certs=<Central Directory>\\trusted.certs deployment.system.security.trusted.certs.locked
Specify the system level deployment properties file in the System-wide config file C:\Windows\Sun\Java\Deployment\itw-deployment.config:
deployment.system.config=file:///<Central Directory>/itw.properties deployment.system.config.mandatory=true
To verify certificates, OWS will now use the central trust store that is specified in the system level deployment properties file.
Customize Application Cache and User Config Location
Centralized location for the configuration and cache can be specified using XDG_CONFIG_HOME and
XDG_CACHE_HOME environment variables.
The centralized configuration comprises:
-
deployment.properties : all users must use the same deployment.properties for OWS
-
user decisions (.appletTrustSettings)
-
logs - logs for the app started by each user
-
security (certificate stores)
-
icons - for the app started by user
The centralized cache comprises
-
jvm_cache : directory where common set of downloaded JVMs are stored (this can be separately configured using the
ows.jvm.manager.cache.dirproperty) -
cache and recently_used file : directory for caching the jnlp and resources of the applications started by users
-
temp dir : Directory created by OWS for temp files.
JVM Management
OWS provides facility to choose set of JVMs that can be used to run the applications specified in JNLP files
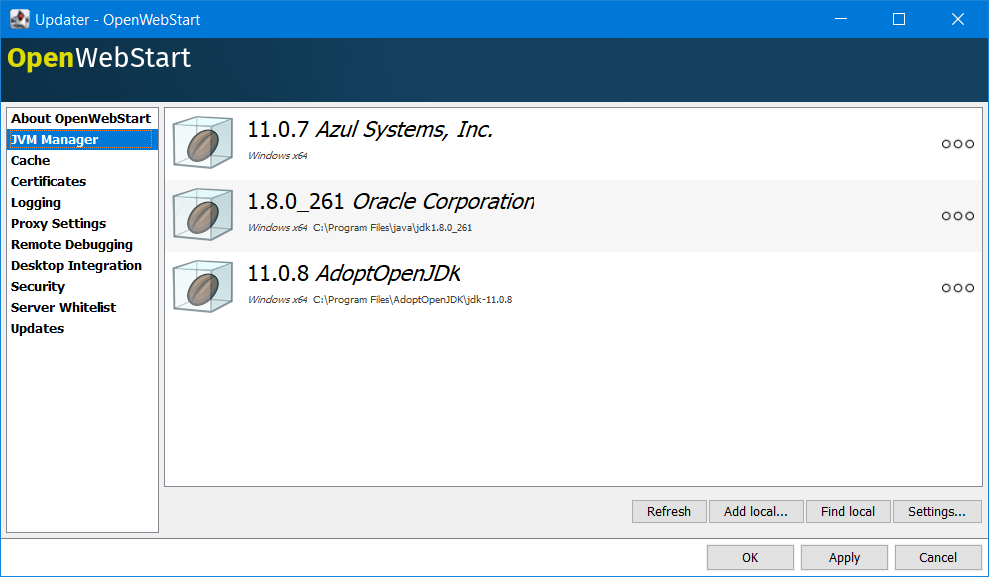
One can choose or automatically add locally available JVMs or one can specify the server from where JVMs can be downloaded.
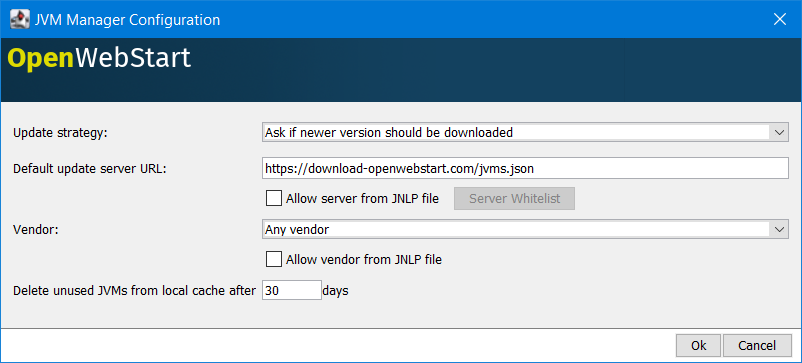
Customize JVM Cache Location
The jvm_cache location can be configured using the property ows.jvm.manager.cache.dir in the deployment.properties file:
ows.jvm.manager.cache.dir=c:\\temp\\JVMCacheDir|
Note
|
ows.jvm.manager.cache.dir specification in deployment.properties takes precedence over XDG_CACHE_HOME.
|
JVM Download Server
OpenWebStart can fetch JVMs and JVM updates from a download server that is specified in the JVM Manager Configuration of the OWS Settings application.
The default points to https://download-openwebstart.com/jvms.json.
Set up a Custom Download Server
If you want to set up your own JVM download server you must provide a json file which lists all available JVMs.
This json file must contain the following data:
{
"cacheTimeInMillis":<miliseconds>,
"runtimes":[
{
"version":<JVM version>,
"vendor":<vendor name>,
"os":<OS identifier>,
"href":<absolute url to the archive containing the JVM>
},
... more runtime definitions
}- cacheTimeInMillis
-
The time which needs to elapse before a client is allowed to contact the server again. Usually the server is accessed once per application startup.
- os
-
Possible values are: MAC64, MAC32, MACARM64, LINUX64, LINUX32, WIN64, WIN32
Allowing JVM Server in JNLP and defining a JVM Server Whitelist
You can allow the specification of JVM server in the JNLP file by defining the property:
ows.jvm.manager.server.allowFromJnlp=true.
In this case the JVM will be downloaded from the URL specified in the JNLP file:
<java version="1.8*" href="http://myjvms.myserver.com/jvms.json"/>When allowing JVM server download from the JNLP file, as a security measure it is advisable to define a whitelist for JVM server URLs that will be specified in JNLP files. JVMs will be allowed to be downloaded from only those server URLs that match a whitelist entry.
The JVM server whitelist can be defined in the deployment properties file:
ows.jvm.manager.server.allowFromJnlp.whitelist=myjvms.myserver.com, *.jvms.comIt is possible to specify wildcards in the URLs specified in the whitelist. Please see the section on "Server Whitelist" for details.
Searching for local JVM
OpenWebStart can search for already installed JVMs on your local file system. This is done by checking in a few default locations. The list of default locations is by no means exhaustive. Thus, it is possible that OpenWebStart will not find all JVMs on the local file system.
There are a few settings which can be used to configure the search for local JVMs. See Configuration Properties Overview for a detailed description of the properties.
ows.jvm.manager.searchLocalAtStartup=true
ows.jvm.manager.excludeDefaultSearchLocation=true
ows.jvm.manager.customSearchLocation=c\:/path/to/jvm,c:\\path\\to\\other\\jvmChoosing the JVM version
OWS starts the JNLP application with the JVM that best matches the JVM specified in the JNLP file.
<java version="1.8+" java-vm-args=" -Xmx512m -Xms128m -XX:SurvivorRatio=6 -XX:NewSize=96m -XX:MinHeapFreeRatio=20 -XX:MaxHeapFreeRatio=30"/>The version number specified can either end with a number, and asterisk or a plus sign.
1.8 would mean the version must be 1.8. 1.8* means anything at or higher than 1.8 but less than 9 (like 1.8.x). 1.8+ means anything 1.8 or higher (such as 11, 17, 21).
Specify a specific JVM vendor in the JNLP file
As illustrated above in figure 4, you can specify a particular vendor that should be taken into consideration for selecting the JVM that launches your JNLP application.
In addition to that, it is possible to specify a JVM vendor in the JNLP file itself:
<java version="1.8*" vendor="AdoptOpenJDK" ... />You can use one of the following vendor names/alias as value for the vendor attribute:
"*" "AdoptOpenJDK", "Adopt" "Amazon.com Inc.", "Amazon Inc.", "Amazon" "Azul Systems, Inc.", "Azul" "BellSoft" "Eclipse Adoptium", "Adoptium" "Oracle Corporation", "Oracle"
The asterix ("*") is the same as if you skip the vendor attribute. It means "any vendor" will be fine. This is the default.
If there is no specific vendor specified in the OWS Settings UI (i.e. "Any Vendor" selected), the vendor attribute specified in the JNLP file will be considered by default.
If no vendor hint is set in OWS Settings and the JNLP does not contain any vendor information, the first JVM is taken that is found in the jvms.json of the download server.
If there is no specific vendor specified in the OWS Settings UI (i.e. "Any Vendor" selected) and if a specific vendor is specified in the JNLP (i.e. vendor="SomeVendor") and if that vendor’s JVM is not available on the JVM download server then OWS will throw "No suitable JVM was found" error.
Note that if there is already a specific vendor selected in the OWS Settings, the vendor information from the JNLP file will only overrule this setting when the configuration property ows.jvm.manager.vendor.allowFromJnlp is set to true.
This policy prevents that the JNLP file vendor details get precedence over OWS Settings.
Specify 32-bit JVM in JNLP file
There is the possibility to advise OpenWebStart to use the 32-bit JVM on a 64-bit machine by specifying the require-32bit attribute in the JNLP file as follows:
<java version="1.8*" require-32bit="true" ... />Whitelist for JVM Arguments
While starting the JVM, OWS passes the JVM arguments specified in the JNLP file:
<java version="1.8+" *java-vm-args=" -Xmx512m -Xms128m -XX:SurvivorRatio=6 -XX:NewSize=96m -XX:MinHeapFreeRatio=20 -XX:MaxHeapFreeRatio=30"*/>Moreover, using the environment variable JAVAWS_VM_ARGS, you can specify JVM arguments that will be applied to all JNLP files in addition to those specified in a JNLP file:
set JAVAWS_VM_ARGS=-Xss2048k -Xmx4096mOWS maintains a hardcoded list of secure JVM arguments as specified at:
OWS allows only those JVM args that are in the above lists.
However, sometimes with new versions of JREs new JVM arguments are introduced.
Also, some desired arguments are not included in the above lists.
In such cases it is possible for the user to specify additional JVM arguments in the deployment.properties for OWS to allow them to be passed to the JVM:
deployment.jvm.arguments.whitelist=-Dnew_jvm_arg1, -Dnew_jvm_arg2Subsequently, the JNLP file and the environment variable JAVAWS_VM_ARGS can include the whitelisted JVM args:
<java version="x" java-vm-args="-Dnew_jvm_arg1=value1 -Dnew_jvm_arg2=value2"/>Note: The whitelist should only contain the name of the JVM argument and not the value as can be seen in the example above.
JNLP file specific JVM Arguments
Sometimes there is a need to add to or override the java vm arguments specified in an unmodifable legacy JNLP file. OWS enables you to specify jnlp specific java vm args in the deployment.properties file.
Suppose you have the following JNLP files for which you want to add to or overide java vm args and properties:
jvm_args_1.jnlp:
<j2se version="1.8*" java-vm-args=" -Xmx512m -Xms256m -Djnlp.ccc=jnlp"/>
<jar href="generated-jars/jvm_args.jar"/>
<property name="http.agent" value="jnlp"/>
<property name="javaws.xyz" value="jnlp"/>
<property name="sun.java2d.dpiaware" value="true"/>
<property name="my.prop" value="jnlp"/>
<property name="jnlp.prop" value="jnlp"/>
</resources>
jvm_args_2.jnlp :
<resources>
<java version="1.8+" java-vm-args="-Xmx512M -Xms256M -Djnlp.ccc=jnlp -Dmy.prop=jnlp --add-modules=java.sql"/>
<jar href="generated-jars/jvm_args.jar"/>
<property name="sun.awt.disableMixing" value="true"/>
<property name="http.agent" value="Blah"/>
<property name="javaws.xyz" value="jnlp"/>
<property name="sun.java2d.dpiaware" value="true"/>
<property name="jnlp.prop" value="jnlp"/>
</resources>In the deployment.properties file specify the vm args that will be merged with the vm args specified in the jnlp file:
ows.jvmargs.for.jvm_args_1.jnlp=-Xmx2048m -Xms512m -Dabc\=dep -Ddepprop=dep -Dmy.prop\=depprop -Djavaws.xyz\=dep -Djnlp.ccc\=dep -Dsun.java2d.dpiaware\=false -Dhttp.agent\=BBBB ows.jvmargs.for.jvm_args_2.jnlp=-Xmx1024m -Ddepprop=dep -Xms512m -Dsun.java2d.dpiawared\=false -Dmy.prop\=depprop -Djavaws.xyz\=dep -Djnlp.ccc\=dep -Dsun.java2d.dpiaware\=false -Dhttp.agent\="BBBB" --add-opens\=java.desktop/sun.print\=ALL-UNNAMED --add-exports\=java.desktop/sun.print\=ALL-UNNAMED --add-modules\=java.sql
Now, when you run the above jnlp files with OWS, you will find that the vm args specified in the deployment.properties for those jnlp files will be appended to the "java-vm-args" and "property" resources specified in that jnlp.
For example, for the given jnlp file jvm_args_1.jnlp, the resulting vm args passed to the JVM that runs the application will be:
-Xmx512m, -Xms256m, -Djnlp.ccc=jnlp, -Djavaws.xyz=jnlp, -Dsun.java2d.dpiaware=true, -Djnlp.prop=jnlp, -Dhttp.agent=jnlp, -Xmx2048m, -Xms512m, -Dabc=dep, -Ddepprop=dep, -Dmy.prop=depprop, -Djavaws.xyz=dep, -Djnlp.ccc=dep, -Dsun.java2d.dpiaware=false, -Dhttp.agent=BBBB
The final vm args will be a union of vm args from Jnlp and deployment.properties. Since the vm args from deployment.properties come later, the common properties like -Xmx, -Xms, http.agent, my.prop will have the values from ows.jvmargs.for.jvm_args_1.jnlp at runtime.
Cache Management
OWS downloads the resources like jars and images specified in the JNLP file from the specified server(s). OWS stores application resources for faster execution by avoiding downloading the next time you run the application. By default, application resources are stored in <User Home>/.cache/icedtea-web/.cache directory. However, OWS will re-download resources for the application if it finds that a resource has been updated on the server.
To find out whether a resource has been modified since the last download, OWS sends an HTTP HEAD request to the server and expects to receive the last modified timestamp of the resource on the server. In order to facilitate caching of resources by OWS it is necessary, that the server from where the resources are downloaded is configured to respond to HTTP HEAD request. In case the server is not configured to respond to HTTP HEAD request, OWS will not be able to determine the last modified timestamp of the resource and will go ahead and download the resource.
The OWS cache can be configured and managed:
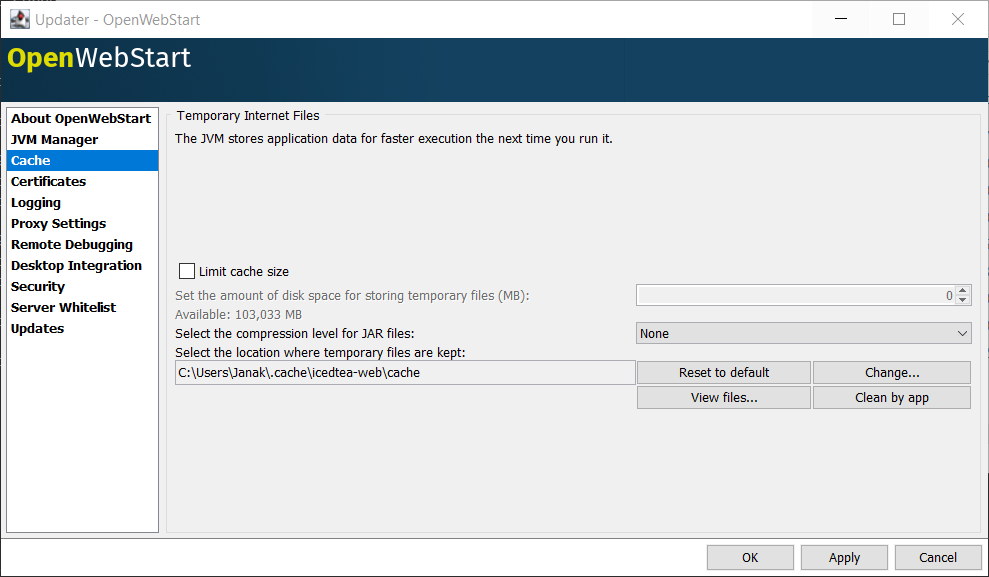
Application Management
An experimental feature has been provided to manage applications downloaded by OWS.
This feature can be enabled by setting the following property in deployment.properties:
ows.experimental.applicationManager.active=true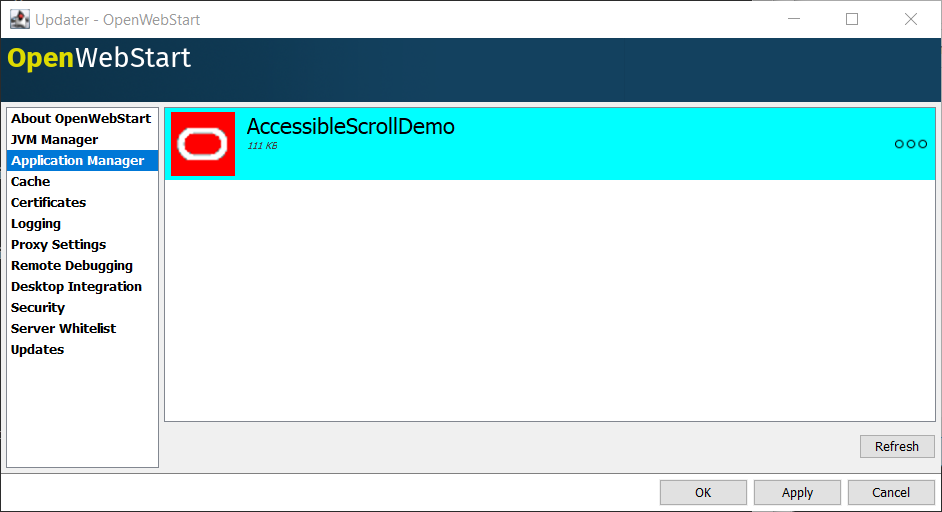
The Application manager shows the list of downloaded applications. It allows to:
-
start the application
-
create a shortcut
-
delete the application from cache
Proxy Settings
It is possible to configure proxy to be used by OWS when it downloads jnlp files and resources. OWS will use these settings to setup a proxy with the java.net package. As a consequence the proxy will also be effective for any connection the application is creating.
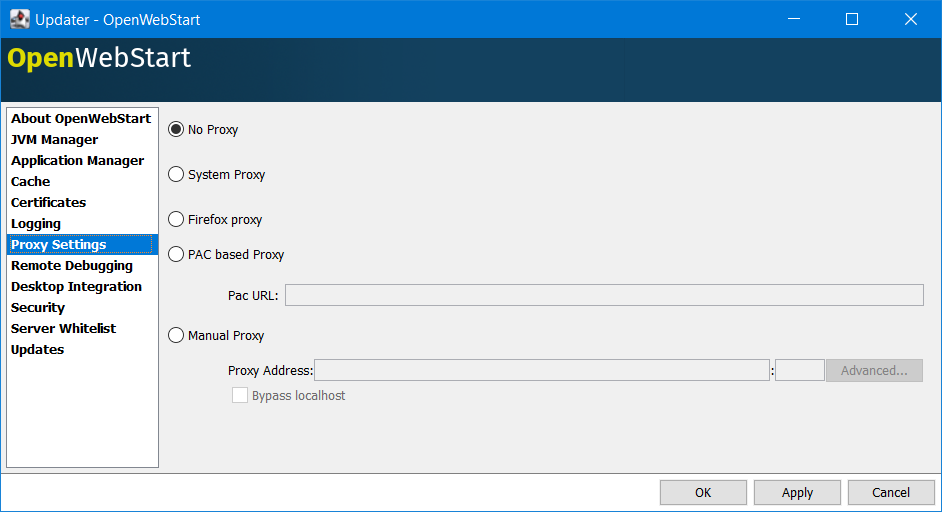
The System Proxy option is trying to imitate the behavior of your operating system (OS) and the proxy settings which are defined there. E.g. for Windows the settings are read from the registry and then converted into a java.net proxy. MacOS and Linux are working in a similar way.
- NOTE
-
It is not possible to delegate the responsibility directly to the OS. Therefore, the behavior of OWS may diverge from the behavior of your OS if System Proxy is selected. One known limitation is on Windows, where there is currently no support for wildcards in the list of excepted servers.
Proxy Auto-Configuration (PAC)
You can specify a PAC proxy. A PAC file is a small JavaScript file that defines rules for choosing the appropriate proxy server for a given URL or request.
OWS uses Mozilla Rhino, an open‑source JavaScript engine, to run the PAC JavaScript.
Sometimes, while processing a complex PAC script, the Rhino Engine may run out of its internal stack memory.
This can be avoided by specifying a JVM argument -Xss, e.g. -Xss2048k, for the JVM used in Stages 1 and 2 of OWS.
For the Stage 1 JVM, specify the JVM argument in the javaws.vmoptions file in the OWS Install directory
For the Stage 2 JVM, specify the JVM argument in either the JNLP file, or the JAVAWS_VM_ARGS environment variable, or
in the deployment.properties file using property for JNLP specific JVM arguments ows.jvmargs.for.
Security Settings
Security settings for OWS can be configured in the Security panel:
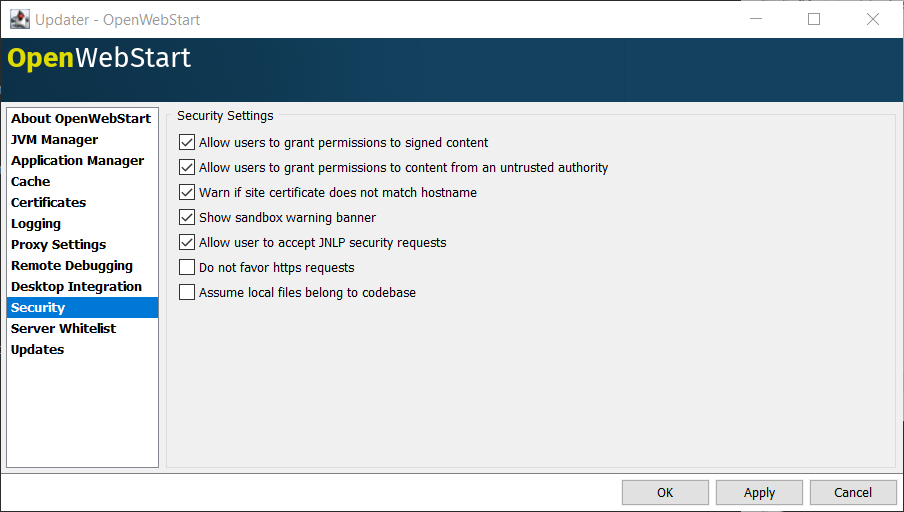
Suppressing security checks on manifest
If security related attributes (such as permissions etc) are missing in the manifest of a signed jar, OWS displays a Security dialog:
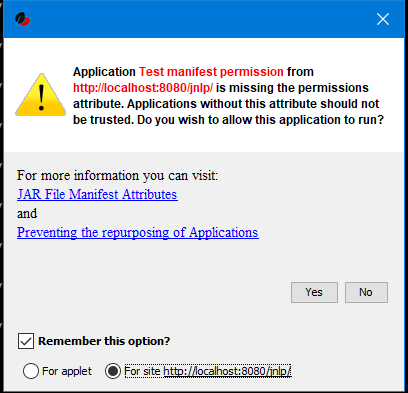
You can choose to "Remember this option" for the site and Press the Yes button.
Your decision will be stored in the file <User_HOME>/.config/icedtea-web\.appletTrustSettings.
Next time when you start the jnlp you will not be shown the above dialog.
Alternatively, you can suppress the checking of selected or all manifest attributes by specifying the following property in your deployment.properties file:
deployment.manifest.attributes.check=NONEDefault value of this property is ALL.
Other values for this property are PERMISSIONS, CODEBASE, TRUSTED, ALAC, ENTRYPOINT.
You can specify a comma separated list of the Manifest attributes to be checked by OWS.
For example if you want all except the PERMISSIONS attribute to be checked by OWS ManifestChecker then you could specify:
deployment.manifest.attributes.check= CODEBASE, TRUSTED, ALAC, ENTRYPOINTCertificates
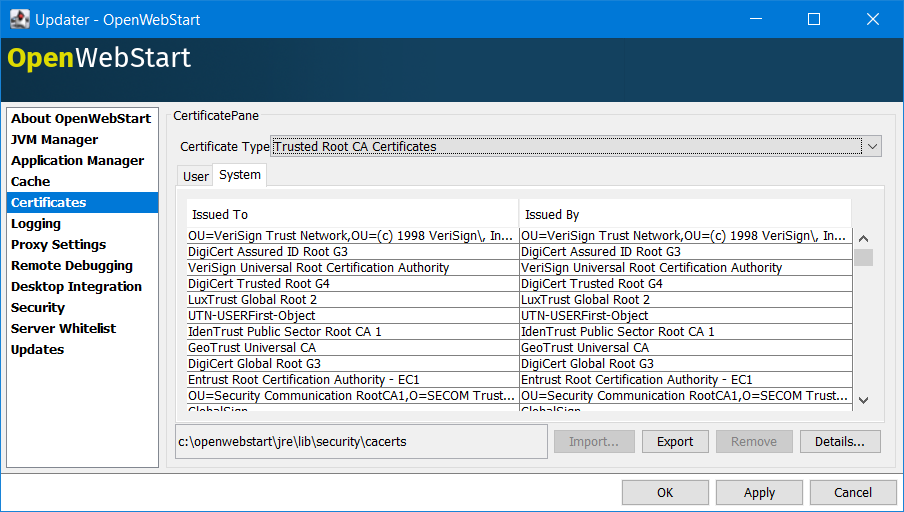
- TIP
-
The System tab of the certificate view shows the certificates included in the embedded JRE. Since a JNLP application will not be launched in this JRE but in one which is managed by the JVM Manager, the certificates available at runtime of the application may differ. The certificate view is also accessible from the Java console. If launched from the Java console the certificate view will show the certificates of the actually running JVM in the System tab. This can be used to check the certificates of the JVM which is executing the application.
If you want to import custom certificates you should do this in the User tab. This will ensure that the certificate is available in any JVM which is launched by OWS.
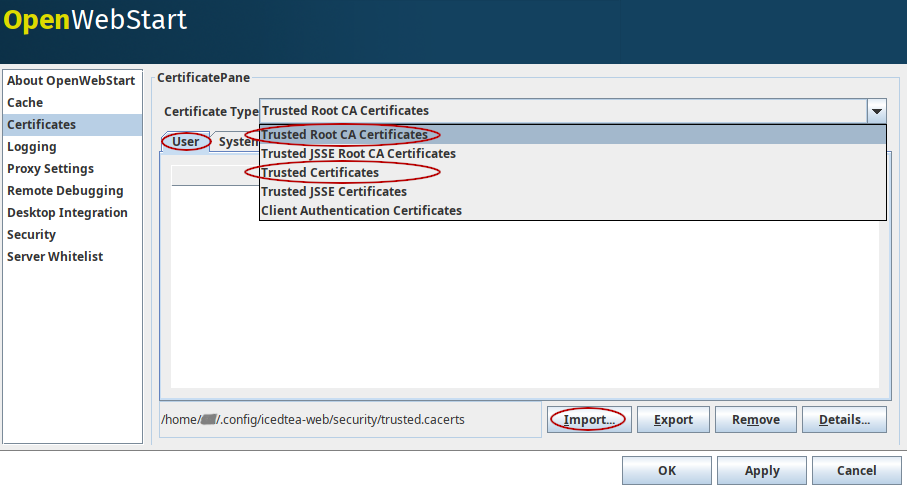
OpenWebStart supports importing of PKCS12 certificates.
Open the settings and go the tab Certificates then select the appropriate user store and hit "import…"
Most likely you will want to import a certificate to the Trusted Certificates or the Trusted Root CA Certificates.
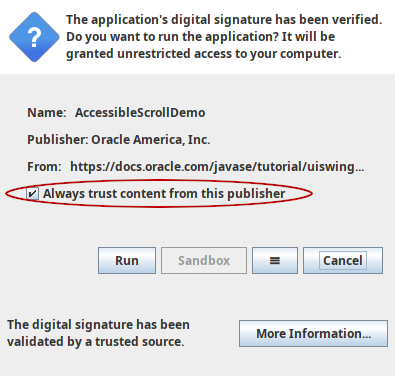
Another possibility is to select the option Always trust content from this publisher
- NOTE
-
OpenWebStart does not maintain a curated collection of certificates by itself. Rather it relies on the JVM which brings a default set of certificates. In this context it is helpful to distinguish between the bundled JVM, used to run OpenWebStart itself, and the custom-selected JVM used to launch the JNLP applications. While the bundled JVM cannot customized or replaced by an OpenWebStart user, the JVM used to run the JNLP application is determined by the definition in the JNLP file and by the configuration of the OpenWebStart JVM Manager. The certificates available during the execution of the JNLP application are those who come with the custom-selected JVM.
Server Whitelist
The "Server Whitelist" panel in OWS settings displays the server whitelist.
To define a server whitelist you have to edit the deployment.properties file in your config directory with a text editor by adding a new line similar to the following:
deployment.security.whitelist=10.10.10.10, google.com, some.server.netThe different servers are listed as a comma separated string. Localhost is implicitly always in the whitelist. If you delete the line again then no whitelisting is applied and all servers are reachable.
Note that whitelisting only applies while downloading resources (jars and jnlps) and not while an application is running. Thus, an application can open a connection to a server which is not in the whitelist.
It is also possible to specify the content of the whitelist in the response file of an unattended OWS installation.
It is possible to specify a wildcard in the host and port part of the URL. The following table illustrates the rules for whitelist URLs in regard to wildcard:
| Whitelist entry | UI Displayed | Comment |
|---|---|---|
only the specified protocol, host port combination is whitelisted |
||
domain.com |
since HTTPS and 443 are defaults |
|
100.101.102.103 |
since HTTPS and 443 are defaults |
|
since HTTP is used default port is 80 |
||
since HTTPS is used default port is 443 |
||
any port is whitelisted |
||
any domain which ends in "domain.com" is whitelisted |
||
*.domain.com:* |
any domain which ends in ".domain.com" and any port is whitelisted |
|
any host but with protocol https and port 443 is whitelisted (any part other than the first part of host cannot be a wildcard) |
||
Error: invalid host |
* is only allowed at position 0 of the host name |
|
Error: invalid host |
for host part use either * or text but not combination |
|
Error: invalid host |
* is only allowed at position 0 of the host name |
|
Error: Invalid port |
only a number in the range 1-65535 or * is valid for the port |
|
Error: Invalid IP Address |
IP address cannot have a wildcard |
|
Error: Invalid IP Address |
IP address cannot have a wildcard |
Logging
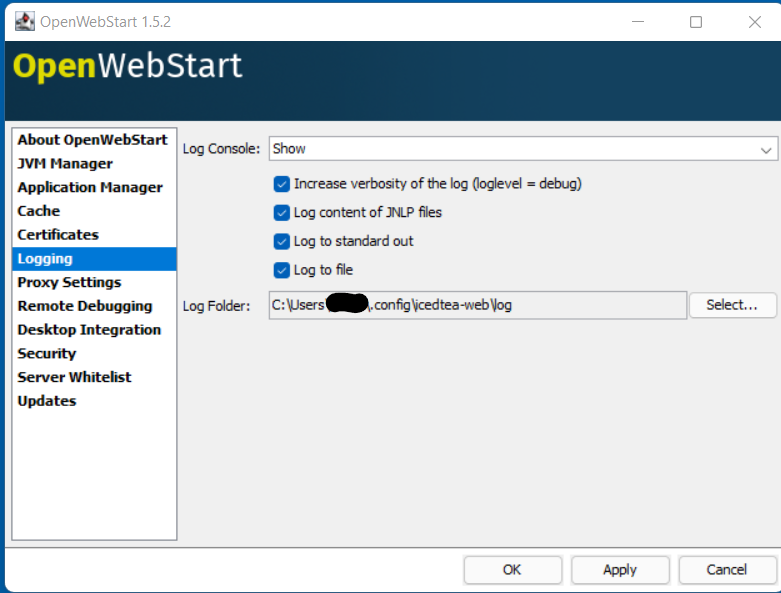
OpenWebStart provides access to log message information to monitor application execution and analyse erroneous behavior by the Log Console GUI and log files. Both can be enabled in the "Logging" panel in OWS settings.
Log Console
OpenWebStart provides the possibility to show a log console window where all log messages of OpenWebStart itself and the launched JNLP application are displayed.
Various filter options can be selected to reduce the log output. To show the log console choose "Show" in "Log Console" selection.
Logging to Files
Logging to files can be activated for file-based log analysis or to send the logs files to the OpenWebStart support.
You have to select "Activate debug logging", "Log to file", and specify the log folder where OpenWebStart should write the log files.
By default, this is <user_home>/.config/icedtea-web/log. Ensure that your folder has write access permissions when customizing this path.
When launching a JNLP application, OpenWebStart produces three log files for different stages. They all following the naming convention:
<timestamp>-ows-stage<stage number>.logThe stage 1 file contains log events on the start-up of OpenWebStart itself. It provides details on version and update status, embedded JVM version, JVM arguments, keystores loaded, validation and parsing results of the JNLP file, and details on the VM required by and used to finally launch the JNLP application. It ends with all the details about the command that OpenWebStart is about to execute to launch the JNLP application in stage 2.
Note: For MacOS there are actually two log files for stage 1. This is due to a technical limitation of the launcher OWS is using. The main log file can easely be determined by its size as it contains more log lines.
The stage 2 file logs the events that happen when OpenWebStart launches the JNLP application. This is probably the most relevant log file for OpenWebStart users. It provides details on how the launch and execution of the JNLP application is going, such as the resources downloaded for the application. If your application cannot start properly, this log file is the best place to look for any error messages or stack traces.
Note that log files of the OpenWebStart Settings application also goes to this log directory. They are named
<timestamp>-ows-settings.log
You will rarely need those.
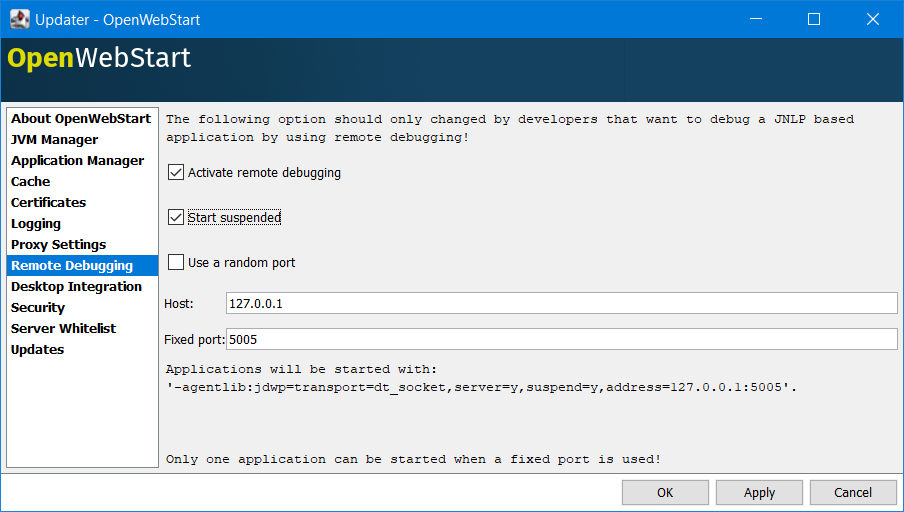
Remote Debugging
OWS allows remote debugging of the application started by OWS. You can configure the settings as follows:
Desktop Integration
OWS allows to specify when and how desktop and start menu shortcuts are created.
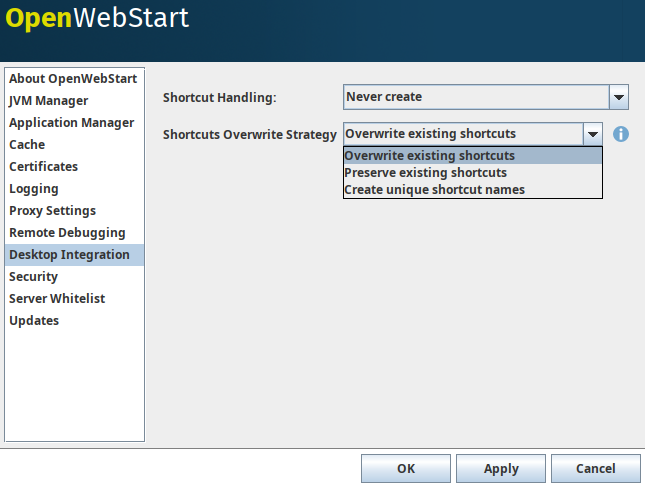
The options for when a shortcut is created are:
-
Never create: Never create a shortcut
-
Always allow: Always create a shortcut
-
Ask user: Shows a dialog to ask user
-
Ask if hinted: Ask user if hinted in jnlp file
-
Always if hinted: Always create when hinted in jnlp file
You may also specify deployment.javaws.shortcut property in the deployment.properties file with values
NEVER, ALWAYS. ASK_USER, ASK_IF_HINTED (default) and ALWAYS_IF_HINTED.
The names of the shortcuts depend on the title or the name of the jnlp file. This may lead to overwriting of the shortcut of one application by the shortcut of another application with the same title or jnlp file name. OWS provides the following strategies for how shortcuts are created:
-
Overwrite: Always overwrite existing shortcuts in case of name clash
-
Preserve: Keep the existing shortcuts in case of name clash
-
Unique Name: Create unique names for shortcuts by appending a hash suffix to prevent name clash.
You may also specify ows.shortcut.update.strategy property in the deployment.properties file with values OVERWRITE (default),
PRESERVE or UNIQUE_NAME.
|
Tip
|
On MacOS, application shortcuts are also added to the Launchpad when shortcut creation is turned on as described above.
If you want to remove some or all of these shortcuts from the Launchpad, you have to delete the corresponding files in the <User Home>/Applications directory.
|
OWS Command Line Arguments
OWS can be started from command line as follows:
- Windows
javaws <path or url of jnlp file>- Mac
open -a "OpenWebStart javaws" <path or url of jnlp file>Some of the command line arguments are described below:
-Xoffline : Start a Jnlp application in Offline mode
The Offline mode means that OWS will not access a server to fetch resources specified in the Jnlp file.
You can start a previously cached Jnlp application in Offline mode using the following command:
- Windows
javaws -Xoffline myApp.jnlp- Mac
open -a "OpenWebStart javaws" myApp.jnlp --args -XofflineIn the above example myapp.jnlp is a previously downloaded and cached Jnlp file. OWS expects that the jars files for the app are available in the cache. For example:
<User Home>/.cache/icedtea-web/cache/0/0/myApp.jarNote that you will get java.net.ConnectException if you run javaws without the -Xoffline parameter when NOT
connected to the server as OWS will try to fetch the resources from the server and fail.
-arg : Passing arguments to the application
- Windows
javaws -arg arg1=value1 arg2=value2 -jnlp <path to jnlp file>- Mac
-
Since the JNLP file or URL comes at the end of that invocation on Mac this requires some argument wrangling. You can passing arguments to the application using the following shell script:
#!/bin/bash
# A wrapper for OpenWebStart that behaves like 'javaws' on MacOS.
if [ "$#" -lt 1 ]; then
echo "Must provide at least a JNLP file or URL"
exit 1
fi
# The JNLP file or URL which much be at the end of the argument list.
jnlp=${!#}
# The rest of the arguments, if there are any.
argarray=("${@:1:$#-1}")
open -a "OpenWebStart javaws" "$jnlp" --args "${argarray[@]}"The specified arguments will be passed to the application’s main method.
-allowredirect : Enable OWS to follow HTTP redirects.
javaws -allowredirect http://jogamp.org/deployment/archive/rc/v2.3.2/jogl-demos/Gears.jnlp-Xclearcache : Clear the Jnlp applications from the cache.
javaws -XclearcacheConfiguration Properties Overview
The following table provides an overview of the configuration properties of OpenWebStart.
|
Note
|
The properties marked in the column LK are lockable. The properties marked in the column RV can be specified in the response.varfile. See Configuration and Unattended Installation for further details. |
| Property | LK | RV | Description |
|---|---|---|---|
ows.jvm.manager.cache.dir |
X |
X |
Allows to specify the directory where the JVM cache is located. The follow example shows two examples for Windows: ows.jvm.manager.cache.dir=c:\\temp\\JVMCacheDir or ows.jvm.manager.cache.dir=c\:/temp/JVMCacheDir |
ows.jvm.manager.cache.cleanup |
X |
X |
Allows to disable the cleanup of the local JVMs. Default is true. The benefit of disabling this is to avoid race conditions if two instances of OWS are launched at exactly the same time. |
ows.jvm.manager.server.default |
X |
X |
This property must contain a valid URL that defines the server that is used to download new JVMs. |
ows.jvm.manager.server.allowFromJnlp |
X |
X |
Defines if a custom URL can be used to download a JVM. Such URL can be part of a JNLP file. |
ows.jvm.manager.server.allowFromJnlp.whitelist |
X |
X |
A comma separated list of urls that are defined as whitelist. The whitelist is checked whenever OpenWebStart will download a JVM from an URL out of a JNLP file. |
ows.jvm.manager.vendor |
X |
X |
Defines a specifc JVM vendor. By doing so, only JVMs from that vendor will be downloaded. You can use ‘*’ to allow any vendor. |
ows.jvm.manager.vendor.allowFromJnlp |
X |
X |
Defines if a vendor attribute in a java/j2se tag of the JNLP file should be respected. If a specific JVM vendor is defined, this is false i.e. the vendor from the settings has precedence by default. If "Any Vendor" is selected in OWS Settings, this property is true to take the vendor hint of the JNLP file into consideration. |
ows.jvm.manager.updateStrategy |
X |
X |
When starting a JNLP application, OpenWebStart can check if an updated JVM is available to run the application. This property defines how OpenWebstart behaves in the JVM check. Possible values are NO_REMOTE (never check the update server), DO_NOTHING_ON_LOCAL_MATCH (do not check for updates on local match but do download if no local match found), ASK_FOR_UPDATE_ON_LOCAL_MATCH (check for update on local match but ask before installing new JVM) and AUTOMATICALLY_DOWNLOAD (check and install for newest JVM) |
ows.jvm.manager.versionRange |
X |
X |
Allows to limit the possible JVM versions. Must be valid version-string according to JSR-56 Appendix A. |
ows.jvm.manager.searchLocalAtStartup |
X |
X |
If set to true OpenWebStart will search for new local JVMs at every start. Default is false. |
ows.jvm.manager.excludeDefaultSearchLocation |
X |
X |
If set to true OpenWebStart will exclude the default locations when searching for JVMs. Default is false. |
ows.jvm.manager.customSearchLocation |
X |
X |
Comma separated list of custom locations to search for JVMs. Default is empty. |
deployment.proxy.http.host |
X |
X |
The HTTP proxy hostname. |
deployment.proxy.https.host |
X |
X |
The HTTPS proxy hostname. |
deployment.proxy.http.port |
X |
X |
The HTTP proxy port. |
deployment.proxy.https.port |
X |
X |
The HTTPS proxy port. |
deployment.proxy.bypass.local |
X |
X |
All local hosts should be bypassed. Default is false. |
deployment.proxy.bypass.list |
X |
X |
A comma separated list of host names that should bypass the proxy. |
deployment.proxy.type |
X |
X |
The proxy type that should be used. Possible values are 0 (no proxy), 1 (manual proxy), 2 (PAC based proxy), 3 (Firefox), 4 (system proxy). Default is 4-System |
deployment.proxy.auto.config.url |
X |
X |
The URL for the proxy auto-config (PAC) file that will be used. |
deployment.proxy.same |
X |
X |
If true use the same web server and port for https and ftp as is configured for http. (This is only valid if deployment.proxy.type = 1 (manual proxy). Default is false. |
deployment.cache.max.size |
X |
X |
The cache maximum size. Default is -1 |
deployment.https.noenforce |
X |
X |
If set to true http urls are not converted to https. Default is false. |
deployment.assumeFileSystemInCodebase |
X |
X |
Defines if files from the local filesystem are always handled as if they would be part of the codebase. |
deployment.manifest.attributes.check |
X |
X |
Defines which checks should be performed for all jars. See Suppressing security checks on manifest for details |
deployment.security.whitelist |
- |
X |
A comma separated list of urls that are defined as whitelist. The whitelist is checked whenever OpenWebStart will download a resource (like a JAR file). |
ows.jvm.manager.maxDaysUnusedInJvmCache |
X |
X |
Max number of days an unused JVM stays in the JVM cache. The default is 30. |
deployment.log |
- |
X |
If set to true debug logging is enabled. Default is false. |
deployment.log.file |
- |
X |
If set to true log is outputted to file. Default is false. |
deployment.log.jnlpFileContent |
- |
X |
If set to true log the contents of Jnlp file. Default is false. |
ows.update.activated |
X |
X |
Defines if OpenWebStart should automatically search for updates. |
ows.checkUpdate |
X |
X |
This property has no effect and is only used to lock functionality in the user interface. If this property is locked, a user cannot manually search for OpenWebStart updates. |
ows.update.strategy.settings |
X |
X |
Defines how often OpenWebStart should search for updates when opening the settings windows. Allowed values are ON_EVERY_START, DAILY, WEEKLY, MONTHLY, and NEVER. |
ows.update.strategy.launch |
X |
X |
Defines how often OpenWebStart should search for updates when starting an application. Allowed values are ON_EVERY_START, DAILY, WEEKLY, MONTHLY, and NEVER. |
deployment.connection.connectTimeout |
X |
HTTP request connect timeout in milliseconds. Default is 10000 ms i.e. 10 s. 0 means infinite wait. |
|
deployment.connection.readTimeout |
X |
HTTP request read timeout in milliseconds. Default is 10000 ms i.e. 10 s. 0 means infinite wait. |
|
deployment.javaws.shortcut , ows.shortcut.update.strategy |
X |
Please see Desktop Integration |
|
deployment.console.startup.mode |
X |
SHOW, HIDE or DISABLE console. Default is DISABLE. |
|
deployment.user.cachedir , deployment.user.logdir |
X |
User defined directory for OWS cache and OWS logs. The path for directory can have a placeholder #USER_HOME_DIR# which will be replaced by the path to the user’s home directory on the system. For example: deployment.user.logdir=#USER_HOME_DIR#\\.config\\ows\\log |
|
deployment.security.itw.disablerestrictedfiles |
X |
Create regular files instead of restricted files if true. Default if false. |
|
deployment.log.console.clientapp |
X |
Log client application''s outputs to console if true. Default if false. If true, may lead to memory leak in console if the application output’s large volume of text. |
|
deployment.nosecurity |
X |
Disable security in OWS. Default is false, i.e., security is enabled by default. If true then java.lang.SecurityManger and java.secutity.Policy are NOT set by OWS. |